Assume a wave f(x) consists of a series of square pulse.  Each pulse has a width ∆x = 100 units, a height of 2 units and the wavelength L of the wave is 200 units.  At t = 0 one wavelength L of the wave is shown in the figure below (displacement versus position).

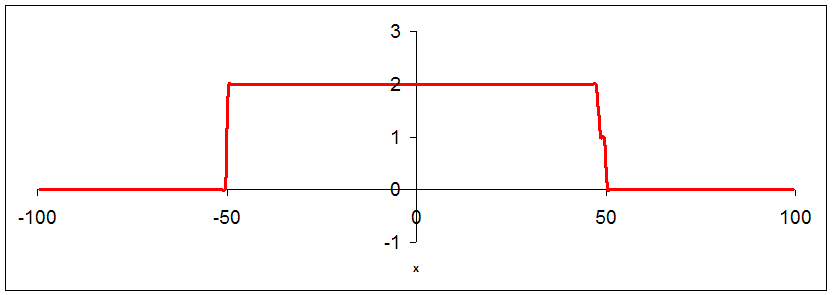
This square wave is a sum of harmonic waves (cosines) with wavelength L/n, n = odd.
f(x) = 1 +  [4/(π)]cos(2πx/L) - 4/(3π)]cos(6πx/L) + 4/(5π)]cos(10πx/L) - 4/(7π)]cos(14πx/L) + 4/(9π)]cos(18πx/L) + 4/(11π)]cos(22πx/L) + ... ,

Download and open the linked spreadsheet.  It contains a plot of these component waves.  The sum column adds the constant term and the cosine wave with period L. 

• In succession add the cosine waves with periods L/3, L/5, L/7, L/9, and L/11 to the sum column and observe how the square wave is synthesized.
• Discuss your observations as each successive term is added with your neighbors.  What happens as you add cosine waves with shorter and shorter wavelengths?